Analysis with R: Assignment 2

LucyTallents · 4 October 2024 14:22

Submit your assignment for the Covariates module in a reply to this topic

Remember to include these five elements:

The results from your best model
Estimates for density, detectability and ESHW, including confidence intervals
Interpretation What conclusion do your draw from your results?
A brief reflection on your next step, challenge you solved, problem you still have or leap of understanding
Give specific and useful feedback to a coursemate

Remember that you can always ask for help or share a draft of your assignment in our course discussion area if you want assistance

Nicorll · 10 October 2024 20:12

#Hypothesis team doing the survey has an influence on detectabilty
#Hypohesis landcover and the team has an influence density

Results of the models;

nPars    AIC delta   AICwt cumltvWt
hntm_LC     4 324.78  0.00 1.0e+00     1.00
hn_tm       3 358.48 33.70 4.8e-08     1.00

 Delta AIC of the hntm_LC cover is zero indicating a good fit. The landcover and the team has an influence on detectability.
 Detectabilty of the covariate team categories i.e team A and team B was done.
Results;

# DetectteamB
Backtransformed linear combination(s) of Detection estimate(s)

 Estimate   SE LinComb (Intercept) TeamB
     90.2 10.1     4.5           1     0

Transformation: exp

# DetectteamA
Backtransformed linear combination(s) of Detection estimate(s)

 Estimate   SE LinComb (Intercept) TeamB
      110 11.7     4.7           1     1

Transformation: exp

The half-normal standard deviation in team B is 90m
In contrast, the half-normal standard deviation in team A is 110m

Detectability is lower for team B.

Confidence intervals

Team B CI		Team A CI
0.025	0.975	0.025	0.975
88.93429	135.1803	72.48405	112.3094

ESWH for team B is 22m
ESWH for team A is 27m

There are overlaps, would it mean that detectability between the two teams is not mutually exclusive? I do understand that both teams did survey in both landcover types.
How do I therefore have the teams and landcover classes separated?

How to calculate detectability of team B in a grassland and Team B in a wetland? I tried this code

 DetectteamBG <- backTransform(linearComb(hntm_LC,
                                         coefficients = c(1, 0),
                                         type = "det"))
DetectteamBG

Error in h(simpleError(msg, call)) :
error in evaluating the argument ‘obj’ in selecting a method for function ‘backTransform’: error in evaluating the argument ‘coefficients’ in selecting a method for function ‘linearComb’: object ‘TeamB’ not found

Nuria · 13 October 2024 01:09

Hypothesis:
a. Team affects detection of water deer
b. Landcover affects density of water deer
1: Model selection table:

           	nPars    AIC    	delta  	    AICwt 	   cumltvWt
hnteam_lc   	4 	324.78  	0.000  		5.0e-01     0.50
hn._lc       	3 	324.81  	0.033	 	5.0e-01     1.00
hnteam_.        3 	358.48 		33.702 		2.4e-08     1.00
hn._.         	2 	361.13 		36.353 		6.4e-09     1.00

hnteam_lc

Call:
distsamp(formula = ~Team ~ Landcover, data = TruncUMF, keyfun = "halfnorm", 
    output = "density", unitsOut = "ha")
Density:
                 		Estimate    	SE     	  z 	 P(>|z|)
(Intercept)         	-2.38 		0.128	 -18.7 	7.86e-78
LandcoverWetland     -1.04 		0.179  	-5.8 	6.57e-09
Detection:
            			Estimate    	SE     	z	 P(>|z|)
(Intercept)    		4.502 		0.112 	40.30   0.000
TeamB         		 0.195 		0.135  	1.44     0.149
AIC: 324.777

Density and Detectability
Density Grassland 0.0924 deer/ha CI: 0.07195514 0.1186252
Density Wetland 0.0328 deer/ha CI: 0.02395455 0.04480861
Detectability Team A 90.2m CI: 72.48405 112.3094
Detectability Team B 110m CI: 88.93429 135.1803
ESWH’s
Detectability Team A 113.08 m and probability to detect 22.62%
Detectability Team B 137.4197 m and probability to detect 27.48%

The best model is the Half-normal with Team and Landcover as covariates, as it has a dAIC of 0, the next model also half-normal with only landcover as covariate also has a very low dAIC, which could indicate that the team does not have much relevance in the model
Both landcovers Grassland and Wetland have a negative estimate, therefore they have less than one deer per ha.
Detectability of Team A is a bit higher than team B

Challenges encountered:

I am having trouble understanding how the hazard-rate function works as in several occasions it gave me Null results.
As well as I still lack some confidence in R to be able to determine the parameters of objects correctly. For example in this exercise, I was not confident on how to calculate ESWH:

What determines the min and max values to use when calculating ESWH for categorical variables?

Nuria · 13 October 2024 01:51

Hi Nicorll,

thanks for sharing your results, I have been able to learn from your approach to the exercise to correct mine.

Regarding to your question I am not sure I can answer, because I don’t think we have considered two covariates influencing one parameter. We have rather worked with one covariate influencing one parameter, having two covariates in our model and two parameters (detectability and density).

Therefore, I think in your results you mention “The landcover and the team has an influence on detectability”, but that is rather two hypothesis if I am not wrong.

The team affects detectability.
The Landcover affects density.

Therefore within your results you might be missing the exploration of the density parameter of the model.

Hope that make sense.

Nicorll · 13 October 2024 04:46

Thank you Nuria, super helpful.

Nuria · 13 October 2024 09:23

Glad if it help, Nicorll. Could you share with me the code you used for the ESWH, or how did you calculated it, please?

Nicorll · 13 October 2024 15:01

Hi @Nuria

this is the code i used


ESHW9 <- integrate(gxhn,
                   0,
                   500,
                   sigma = DetectteamB@estimate)
ESHW9
ESHW9$value / 500


ESHW10 <- integrate(gxhn,
                   0,
                   500,
                   sigma = DetectteamA@estimate)
ESHW10
ESHW10$value / 500

Nuria · 14 October 2024 14:36

Thank you, I now identified the mistake.

sausilwal · 28 October 2024 19:50

Hypotheses:
• Landcover effects detectability by different teams
• Landcover determines density of deer
I have had trouble getting the code right. Thanks to all of your great posts. They helped quite a bit.
I got the following results for half normal and hazard detection functions for the land cover and team covariates.
I am still not quite sure about the ESHW function.
Nuria, what is the meaning of ESHW9 and ESHW 10? Sorry for the late post. I know most of you have already moved ahead.
Further Challenges:
• I couldn’t get Team A and Team B CI separately.
Therefore, I need to,
• Refine the codes according to the covariate hypothesis
• Interpret covariate and ESHW function outputs.
• Identify mistakes

ModSelect
          nPars    AIC  delta   AICwt cumltvWt
hnLC_.         3 271.39   0.00 9.8e-01     0.98
hazLC_.        4 279.16   7.77 2.0e-02     1.00
hnLC_Team      4 324.78  53.39 2.5e-12     1.00
haz._.         3 352.00  80.61 3.1e-18     1.00
hn._.          2 361.13  89.74 3.2e-20     1.00
hn._Team       3 363.11  91.72 1.2e-20     1.00
haz._Team      4 408.82 137.43 1.4e-30     1.00
hazLC_Team     5 410.82 139.43 5.2e-31     1.00

Due to the smaller AIC value, hnLC_Team would be the best-fit model to explain the result of the landcover and team covariate analysis.

ESHW9
1.523077 with absolute error < 8.6e-07

ESHW10
113.0809 with absolute error < 6e-07

hnLC_Team # show model output
Call:
distsamp(formula = ~Team ~ Landcover, data = TruncUMF, keyfun = "halfnorm", 
    output = "density", unitsOut = "ha")

Density:
                 Estimate    SE     z  P(>|z|)
(Intercept)         -2.38 0.128 -18.7 7.86e-78
LandcoverWetland    -1.04 0.179  -5.8 6.57e-09

Detection:
            Estimate    SE     z P(>|z|)
(Intercept)    4.502 0.112 40.30   0.000
TeamB          0.195 0.135  1.44   0.149
AIC: 324.777 

hazLC_Team # show model output

Call:
distsamp(formula = ~Landcover ~ Team, data = TruncUMF, keyfun = "hazard", 
    output = "density", unitsOut = "ha")

Density:
            Estimate    SE       z   P(>|z|)
(Intercept)  -2.9895 0.127 -23.567 8.42e-123
TeamB        -0.0218 0.171  -0.127  8.99e-01

Detection:
                 Estimate  SE       z P(>|z|)
(Intercept)         -7.35 NaN     NaN     NaN
LandcoverWetland    -9.47 300 -0.0315   0.975

Hazard-rate(scale):
 Estimate    SE     z  P(>|z|)
      -12 0.649 -18.4 5.67e-76

AIC: 410.8178

Matt_Gudge · 29 October 2024 11:51

Hypotheses

#1 Survey team affects detectability of water deer

#2 Landcover affects density of water deer

#3 Modelled with both half-normal and hazard detection functions

The model that is the best fit for the data is the global model (i.e a combination of both hypothesis 1 and 2) when detection is modelled by a half-normal curve, this is because this model has a delta of 0 and the lowest AIC. The model hn._LC is a strong competitor as it also has a low AIC and a delta close to 0 with 0.033. This suggests that whilst the data supports both hypotheses, there is stronger support for hypothesis 2, Landcover affects density of water deer.

Detectabilty:

The half-normal standard deviation for Team A is 90.2m, in contrast the half-normal standard deviation for Team B is 110m. Team B’s detectability is higher than Team A’s.

CI’s

DetTeamA_CI
0.025 0.975
72.48405 112.3094
DetTeamB_CI
0.025 0.975
88.93429 135.1803

ESHW

ESHWTeamA
111.4124 with absolute error < 1.2e-12
ESHWTeamB
131.2631 with absolute error < 1.5e-12
ESHWTeamA$value/220
[1] 0.5064199 Detection probability for Team A within 220m from the transect is 50.6%
ESHWTeamB$value/220
[1] 0.5966503 Detecttion probability for Team B within 220m from the transect is 59.7%

Density:
The density estimate for water in grassland is 0.09 water deer per hectare (or 9 per square kilometre). The density estimate for water deer in wetland is 0.03 water deer per hectare (or 3 per square kilometre). The density estimate of water deer in grassland is three times more than in wetland. This is strong evidence for hypothesis #2. This is further supported when we look at the confidence intervals of the two land cover classes, as they do not overlap.

DensGrass_CI
0.025 0.975
0.07195514 0.1186252
DensWet_CI
0.025 0.975
0.02395455 0.04480861

Challenge:

The confidence intervals for detectability of Team A and Team B do not overlap, suggesting no significant difference between the two groups. If this is true, why is it in model with the best fit?

LucyTallents · 11 November 2024 15:17

Yes, if the 95% confidence intervals for the two teams overlap, it means there is weaker evidence for a difference in detection skill between teams

To differentiate between the effects of team and landcover, you need to include models that only contain individual variables. In other words, your full model set should include:

~1, ~1
~Team, ~1
~1, ~Landcover
~Team, ~Landcover

Then you can separate out the effects of each variable, by seeing which model performs the best; comparing models with/without a variable using evidence ratios etc

LucyTallents · 11 November 2024 15:27

Detectability is identical in grassland and wetland in your best model, because you have only included Landcover as a predictor of density, not detectability

I’m not sure why you’re getting that error message. I ran the following and didn’t get an error

DetectTeamA <- backTransform(linearComb(hnTeam_LC,
    coefficients = c(1, 0),
    type = "det"))
DetectTeamB <- backTransform(linearComb(hnTeam_LC,
    coefficients = c(1, 1),
    type = "det"))
DetectTeamA
DetectTeamB

Note that your code is requesting a backtransform for the intercept only, which refers to Team A, not Team B

LucyTallents · 11 November 2024 15:42

Two covariates influencing one parameter

To model multiple covariates influencing a single parameter, you can chain them together with a plus + sign in your model equation. For example, to test whether density is affected by both Distance to coast and Landcover:

hn._DtcLc <- distsamp(~1 ~DistToCoast + Landcover, TruncUMF, keyfun="halfnorm", output="density", unitsOut="ha")

Hazard-rate function

Re your questions about the Hazard-rate function, does my mini-explanation here help?

Calculating ESHW

The ESHW formula always uses zero as the min value and your truncation distance as the max value. It’s the use of model- and category-specific detectability estimates (sigma) that gives you different ESHW estimates for different categories

Does that make sense? I think @Nicorll 's helpful answer clarified it for you

LucyTallents · 11 November 2024 16:07

Take care with the order of covariates in your model formula, @sausilwal ! In your half-normal model, you correctly assign Team as a predictor of detectability:

However, in your hazard rate model, you have the two covariates in the wrong order, so that you’re testing whether Survey team had an effect on density, which is not a valid hypothesis:

It’s an easy mistake to make, but a costly one

It will help to write the covariates in the correct order in your model names - always put the detectability covariates first, i.e. hazTeam_LC instead of hazLC_Team

Can you re-run the model set and post your results again, to complete this assignment?
Do you have any specific questions arising from your reflection about next steps and clarifications?

LucyTallents · 11 November 2024 16:16

Good question, Matt! My interpretation is that Landcover has such a strong effect (and the half-normal curve is so much better fit than hazard-rate to these data) that Landcover carries models containing it up to the top of the AIC table, even though the other variable is not informative. This can be confirmed by calculating summed model weights and evidence ratios, as we do in the final module

I think you mean that they do overlap? ↩︎

sausilwal · 12 November 2024 10:10

Thank you for pointing out the mistake.

Re-run model select Table

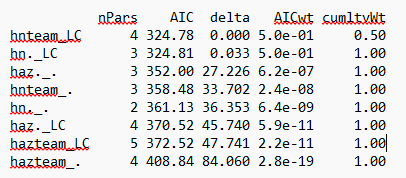
ModSelect
           nPars    AIC  delta   AICwt cumltvWt
hnLC_.         3 271.39   0.00 1.0e+00     1.00
hnLC_Team      4 324.78  53.39 2.6e-12     1.00
haz._.         3 352.00  80.61 3.1e-18     1.00
hn._.          2 361.13  89.74 3.3e-20     1.00
hn._Team       3 363.11  91.72 1.2e-20     1.00
haz._LC        4 370.52  99.13 3.0e-22     1.00
hazTeam_LC     5 372.52 101.13 1.1e-22     1.00
hazTeam_.      4 408.84 137.45 1.4e-30     1.00

Call:
distsamp(formula = ~Team ~ Landcover, data = TruncUMF, keyfun = "halfnorm", 
    output = "density", unitsOut = "ha")

Density:
                 Estimate    SE     z  P(>|z|)
(Intercept)         -2.38 0.128 -18.7 7.86e-78
LandcoverWetland    -1.04 0.179  -5.8 6.57e-09

Detection:
            Estimate    SE     z P(>|z|)
(Intercept)    4.502 0.112 40.30   0.000
TeamB          0.195 0.135  1.44   0.149

AIC: 324.777

hazTeam_LC # show model output

Call:
distsamp(formula = ~Team ~ Landcover, data = TruncUMF, keyfun = "hazard", 
    output = "density", unitsOut = "ha")

Density:
                 Estimate    SE      z   P(>|z|)
(Intercept)         -2.49 0.105 -23.60 3.47e-123
LandcoverWetland    -1.07 0.178  -6.01  1.89e-09

Detection:
            Estimate   SE        z P(>|z|)
(Intercept)   -11.08 4099 -0.00270   0.998
TeamB          -8.88 2892 -0.00307   0.998

Hazard-rate(scale):
 Estimate  SE   z P(>|z|)
    -14.4 NaN NaN     NaN

AIC: 372.5179

Question 1: The detection and density estimate outputs only show assessments for one category (e.g., Wetland and Team B). How do you get estimate outputs for grassland and team A?

I also tried evaluating the covariate models:
Model selection based on AIC:

           K    AIC Delta_AIC AICWt Cum.Wt      LL
hnLC_.     3 271.39      0.00     1      1 -132.70
hnLC_Team  4 324.78     53.39     0      1 -158.39
haz._.     3 352.00     80.61     0      1 -173.00
hn._.      2 361.13     89.74     0      1 -178.56
hn._Team   3 363.11     91.72     0      1 -178.56
haz._LC    4 370.52     99.13     0      1 -181.26
hazTeam_LC 5 372.52    101.13     0      1 -181.26
hazTeam_.  4 408.84    137.45     0      1 -200.42

Model selection based on AICc:

           K   AICc Delta_AICc AICcWt Cum.Wt      LL
hnLC_.     3 274.39       0.00      1      1 -132.70
hnLC_Team  4 330.49      56.10      0      1 -158.39
haz._.     3 355.00      80.61      0      1 -173.00
hn._.      2 362.46      88.07      0      1 -178.56
hn._Team   3 366.11      91.72      0      1 -178.56
haz._LC    4 376.23     101.84      0      1 -181.26
hazTeam_LC 5 382.52     108.13      0      1 -181.26
hazTeam_.  4 414.55     140.16      0      1 -200.42

Model selection based on QAICc:
(c-hat estimate = 1.679429)

           K  QAICc Delta_QAICc QAICcWt Cum.Wt Quasi.LL
hnLC_.     4 171.74        0.00       1      1   -79.01
hnLC_Team  5 208.62       36.88       0      1   -94.31
haz._.     4 219.74       48.00       0      1  -103.01
hn._.      3 221.65       49.91       0      1  -106.32
hn._Team   4 226.35       54.62       0      1  -106.32
haz._LC    5 235.86       64.12       0      1  -107.93
hazTeam_LC 6 244.66       72.92       0      1  -107.93
hazTeam_.  5 258.67       86.94       0      1  -119.34

Further problem: I couldn’t get the code right for the summed model weight for team and landcover covariates.

LucyTallents · 12 November 2024 12:15

Well done! Your model order is different from those above, but that is possibly due to you using a different truncation distance

The only part missing from your assignment now is your estimates from your best model:

Note that I’m looking for the back-transformed estimates, which are easier to interpret and have greater ecological meaning than the covariate coefficient estimates you report above

To answer your questions:

The coefficient estimate for the intercept (provided in the model output) is the estimate for Grassland or Team A, while the value for Wetland or Team B must be calculated from the intercept plus the coefficients provided for Wetland or Team B. We have to back-transform these coefficients to gain meaningful values for detectability and density in the different categories

Review the slideshow on Interpreting coefficients in the Covariates module for a reminder of how to do this

Can you share the code you tried using, and what errors you got?

The conclusions are actually quite simple based on your AIC comparison tables above, so in this example, summing the model weights using our equation isn’t necessary

Your top model contains only Landcover, and has all of the AICwt, which means that:

Models containing Landcover have a summed model weight of 1
Models containing Team have a summed model weight of 0

LucyTallents · 15 November 2024 11:09

A post was split to a new topic: Calculating summed model weights